How to Find the Area of a Circle – A Simple and Comprehensive Guide
-
 Emily Carter
Emily Carter - 23 Jul, 2024

Understanding how to find the area of a circle is a fundamental concept in geometry. Whether you’re a student, a teacher, or just someone interested in math, this guide will walk you through the process step-by-step. We’ll explain the formula, provide examples, and offer tips to help you master this essential math skill.
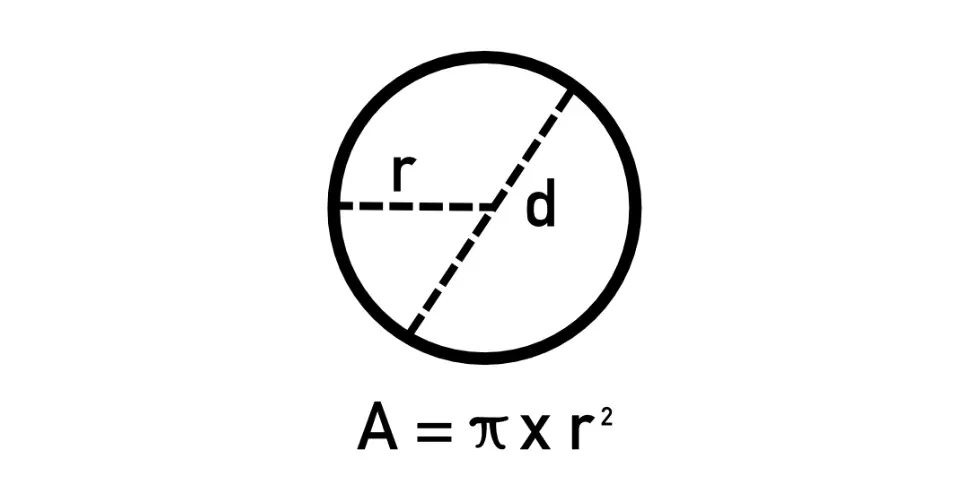
What is the Area of a Circle?
The area of a circle is the amount of space enclosed within its circumference. It’s measured in square units, such as square centimeters (cm²), square meters (m²), or square inches (in²).
The Formula for the Area of a Circle
The formula to calculate the area of a circle is: [ A = \pi r^2 ]
Where:
- ( A ) is the area
- ( \pi ) (pi) is a constant approximately equal to 3.14159
- ( r ) is the radius of the circle
Understanding the Radius
The radius of a circle is the distance from the center of the circle to any point on its circumference. It is half the length of the diameter, which is the distance across the circle through its center.
[ r = \frac{d}{2} ]
Where:
- ( r ) is the radius
- ( d ) is the diameter
Step-by-Step Guide to Finding the Area of a Circle
Step 1: Measure the Radius
Measure the radius of the circle. If you have the diameter, divide it by 2 to get the radius.
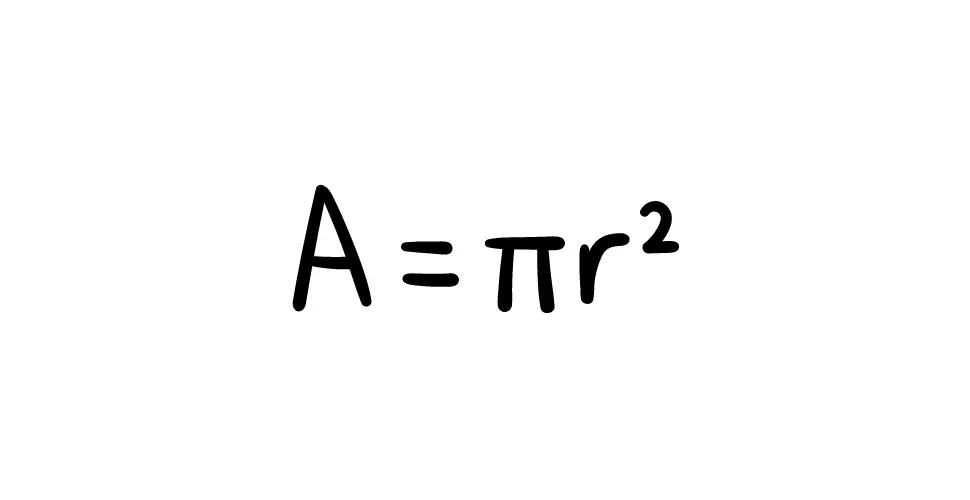
Step 2: Square the Radius
Multiply the radius by itself to get the square of the radius.
[ r^2 ]
Step 3: Multiply by Pi
Multiply the squared radius by ( \pi ) (pi) to get the area.
[ A = \pi r^2 ]
Example Calculation
Let’s go through an example to illustrate how to use the formula.
Example 1: Given Radius
If the radius of a circle is 5 cm, the area is calculated as follows:
[ A = \pi \times 5^2 ] [ A = \pi \times 25 ] [ A \approx 3.14159 \times 25 ] [ A \approx 78.54 , \text{cm}^2 ]
Example 2: Given Diameter
If the diameter of a circle is 10 cm, first find the radius:
[ r = \frac{10}{2} = 5 , \text{cm} ]
Then use the formula to find the area:
[ A = \pi \times 5^2 ] [ A = \pi \times 25 ] [ A \approx 3.14159 \times 25 ] [ A \approx 78.54 , \text{cm}^2 ]
Tips for Finding the Area of a Circle
- Use a calculator: For more accurate results, especially when dealing with pi.
- Double-check your measurements: Ensure that the radius or diameter is measured accurately.
- Practice with different values: This helps reinforce the concept and improve your calculation skills.

Summary
Finding the area of a circle involves using the formula ( A = \pi r^2 ). By measuring the radius, squaring it, and multiplying by pi, you can easily determine the area. Whether you’re working with a given radius or diameter, the process is straightforward and essential for many applications in geometry and beyond.

